Download PDF
Big data, a once-niche buzzword, has become mainstream. And its wealth of clinical and patient information—from electronic health records (EHRs), health insurance and Medicare claims databases, clinical data registries, national biobanks, and mobile and wearable devices—has spawned a boom in population-based research. The ophthalmic literature is now flooded with studies that incorporate patient cohorts in the millions—datasets that are too large for traditional statistical methodologies.
Consequently, many physicians find themselves reading literature that involves unfamiliar data analysis techniques, said Marion R. Munk, MD, PhD, at the University of Bern in Switzerland, and this increasing complexity is now becoming an issue for the practicing ophthalmologist.
A 2014 review of the peer-reviewed ophthalmic literature, for example, found that a reader with basic statistical knowledge was only able to critically evaluate 20% of studies.1 To successfully assess the results of more than 90% required a working knowledge of at least 29 different statistical methods. “Seven years have passed since that publication,” said Dr. Munk, “and it’s safe to say that big data might be pushing many of us into murky waters.”
So the next time you come across a paper investigating the efficacy of treatments X, Y, and Z distilled from hundreds of thousands of patients, how can you decipher when the analysis is sound and when the data are being misused? Here’s what to watch for when navigating big data.
Use Care When Interpreting Significance
Commonly, readers of big data studies misunderstand the word “significance,” said Aaron Y. Lee, MD, MSc, at the University of Washington in Seattle. “Too often, readers conflate statistical significance with clinical significance, and that confusion largely stems from not truly understanding what a ‘p’ value measures,” he said.
P basics. P value is a commonly used measurement of statistical significance, said Dr. Lee. Readers need to be aware that it measures the probability that a study’s result is due to chance and does not necessarily demonstrate a treatment effect of clinical significance. For example, the traditional cutoff for a statistically significant p value is 0.05. P < 0.05 means there’s less than a 5% possibility that the result is a random event.
P meets big data. What’s more, because statistical significance is positively correlated with sample size, these conventional metrics break down when used in large population-based research, said Dr. Lee. “P values were never designed to be used with millions and millions of patients. Now we have the ability to obtain so much data that achieving statistical difference between groups has become almost trivial—seemingly everything becomes statistically significant.”
So when you come across a big data study and see multiple p values that are all extraordinarily small, you might be led to believe there are very strong associations there, he said, when in fact it’s just an artifact of the number of patients included.
When is it clinically significant? While p values are important, readers need to take a deeper look at the size of the real treatment effect that would connote clinical significance, said Maureen G. Maguire, PhD, FARVO, at the University of Pennsylvania in Philadelphia.
Sample scenario. For example, a glaucoma study might look at the effect of two drugs on lowering the intraocular pressure (IOP) of 100,000 patients. Drug A decreased IOP by 5 mm Hg and drug B by 5.1 mm Hg—a mean difference of 0.1 mm Hg. With a p value well below the conventional 0.05 threshold, the researchers found the difference to be highly statistically significant.
“But as the reader, you have to dig in a bit more,” said Dr. Maguire. “That p value only tells you whether the difference between the two drugs is zero or not. It doesn’t tell you anything about how big the difference is.” For that you need to look for effect estimates with corresponding confidence intervals to interpret whether the difference is meaningful, she said. “In this example, let’s say the confidence interval is 0.05 to 0.15 mm Hg,” said Dr. Maguire. “That’s the range of values in which we are fairly sure our mean IOP difference lies. Is that clinically meaningful? No. That’s not going to drive a change in treatment.”
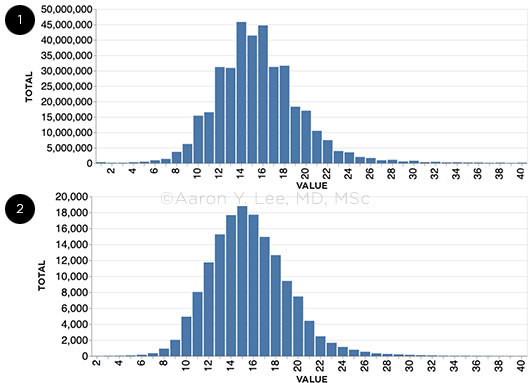 |
|
DATA FROM THE ENTIRE IRIS REGISTRY DATABASE. (1) Goldmann applanation tonometry compared with (2) other forms of tonometry shows that pressures of 12, 14, 16, 18, and 20 are much more common than 13, 15, 17, and 19. Why? Because applanation tonometers are marked for the even numbers, and ophthalmologists tend to round up or down to the nearest even number.
|
Were the Researchers Fishing for P Values?
With the sheer amount of information available from resources like health insurance databases, researchers are better able to investigate multiple hypotheses, said Dr. Munk. But the more statistical tests they employ on a single dataset, the better the chance they will draw an erroneous conclusion.
Errors of commission and omission. In understanding p values, it is critical to frame the hypothesis—the question under investigation. Many questions in medical research involve determining differences between subpopulations. Did patients receiving treatment X have a different outcome than patients receiving treatment Y? Is group X at higher risk of disease than group Y? The null hypothesis states that there is no difference between groups and is akin to “innocence before proof of guilt” in a criminal trial. Two types of errors can occur in reaching a conclusion about the null hypothesis. It can be rejected due to spurious data—a Type I error, akin to convicting an innocent defendant due to chance circumstantial evidence. Alternatively, the null hypothesis can be accepted when it is actually false, a Type II error comparable to acquitting a guilty defendant.
False positives. At the conventional p threshold of 0.05, a single statistical hypothesis has a 1 in 20 probability of significance due to chance—in other words, a 5% chance that it will produce a false positive. This probability dramatically increases as the number of tests increase. For example, testing 14 individual hypotheses on the same dataset using the p threshold of 0.05 will result in a greater than 50% chance of one false positive, and thus a Type I error.2
P-hacking. This is what statisticians call the multiple testing problem, said Dr. Munk, and it can lead to the purposeful misuse of the data, otherwise known as data dredging or p-hacking, in which researchers conduct arbitrary post hoc analyses searching for any type of reportable outcome if their original hypothesis didn’t pan out.
“Massive datasets allow researchers to conduct so many different types of association tests, but they might also be falsely discovering importance,” said Dr. Munk. “Ophthalmologists, for example, can search for relationships by gender, age group, race, presenting visual acuity, IOP, and on and on, but exhaustively testing multiple hypotheses to see what sticks on the wall can be very misleading.”
As a reader, Dr. Munk wants to see clearly formulated, prespecified research questions as well as detailed methods that the researchers have used to conclusively prove or reject each hypothesis. “But if you open a journal and you’re staring down at tables with 50, 60, 70 p values and the writers are correlating everything with everything, you should be cautious,” she said. “That’s definitely a sign of fishing for significance.”
A fix. If the probability of false positives increases as the number of statistical comparisons increase, how can researchers correct for this phenomenon? The simplest method is using a Bonferroni correction, said Dr. Lee, in which the probability threshold (here using the conventional cutoff of 5%) for each individual test is adjusted to 0.05/N (where N is the total number of tests performed), thus ensuring that the study-wide error rate remains at 0.05.
However, this method may also increase the researcher’s risk of an inadvertent Type II error, failing to reject a false null hypothesis. Because reducing the risk of false positives can also increase the risk of missing true positives, many critics believe the Bonferroni correction to be too conservative, said Dr. Lee. “Regardless of what method a researcher uses, by correcting for multiple comparisons, readers can worry less about the false discoveries and spurious associations that the researcher might have produced from slicing and dicing the data,” he said.
Unfortunately, the use of correction factors by ophthalmologists may not be as prevalent as might be expected, added Dr. Lee. For example, in a 2012 review of more than 6,000 abstracts from a major ophthalmic research conference, 8% of the submissions reported at least five p values, 95% of which did not correct for multiple comparisons. In a statistical simulation, the authors estimated that failure to do so could have resulted in 185 false-positive outcomes.2
Visualizing Big Data
Given the size of big data, researchers may represent their datasets in a number of ways for easier consumption. But these pictures can say a thousand words, or none at all, said Dr. Lee.
“For example, you probably won’t come across many bar graphs in this type of research because of their simplicity,” he said. “Data transparency is paramount, and a basic distribution plot showing mean values with standard deviations is going to hide a lot of the messiness that needs to be visible to the reader.”
To provide the fullest picture of variability, current best practice is to present as much of the data as possible, oftentimes with the help of box-and-whisker or violin plots, said Dr. Lee.
Distribution plots. To visualize multiple statistical components of the data, the box-and-whisker plot (Fig. 3) provides a five-part graphical snapshot, including:
- a “box,” which shows the median and the first and third quartiles of the dataset, and
- two “whiskers,” which extend outward from each quartile and represent the minimum and maximum data points.
These plots are helpful because they can provide insight into the outliers (represented by dots), any symmetry and grouping, and how the data skews, said Dr. Lee. They’re limited in value, though, because they don’t show how all of the data points are distributed around these five markers.
The best picture. Likewise, violin plots (Fig. 4) include a snapshot of the median and the interquartile range, said Dr. Lee. But they are extremely useful because they show the full distribution of the data via overlaid density curves—what gives the plot its “violin” shape.
It’s an easy-to-read representation, said Dr. Lee, because the width of the violin corresponds to the frequency of the values along each region of the internal box plot. “This method allows for transparency of the raw distributions for all of the variables in your study. It provides the entire data story.”
Figure 3. Bemme S et al. Ophthalmol Sci. 2021. 100031. Figure 4. Boland MV et al. Ophthalmology. 2019;126:928-934.
|
Be Aware of Treatment and Patient Bias
Readers should also have a healthy skepticism about any bias that researchers unwillingly—or purposefully—introduce in these big data studies, said Dr. Maguire, especially in terms of treatment and patient selection.
Scenario #1: Treatment selection. Imagine a retina study looking at the use of anti-VEGF drugs A and B for the treatment of neovascular age-related macular degeneration (AMD), said Dr. Maguire. The researchers want to know whether the number of injections needed for each drug is the same. A good source of data for this hypothesis would be an insurance claims database, which captures each injection based on specific billing and diagnostic codes.
But what could those data be hiding from the reader? More than you might think, said Dr. Maguire. First, there’s likely no information regarding the size of the neovascular lesion, whether it was classic or occult, or the amount of retina fluid on OCT, she said. “Also, certain ophthalmologists might favor a specific treatment for a specific patient. For example, they might select anti-VEGF drug A, which they think is the best at drying the retina, for patients who have the highest likelihood of requiring multiple injections.”
In doing so, they would overload drug group A with patients who have the worst prognosis so that the average number of injections would be greater than for drug group B, said Dr. Maguire. But a data analyst alone would never know this by just looking at the claims data, she said. And that’s the problem: the bias toward using drug A in worst cases. On the other hand, a randomized masked trial between the drugs, in which the severity of cases was identical, might reach the conclusion that the two drugs are equally effective. “The reader who is accustomed to reading randomized controlled trials might assume that all of the patients in the claims database were of the same need for injections. So to create an even playing field, a study like this would require collaboration with a retina specialist to identify potential selection factors and provide insight into the likely magnitude of treatment bias.”
Scenario #2: Patient selection. When selecting groups of patients who will undergo analysis, some exclusions that sound very reasonable can also cause trouble when interpreting results, said Dr. Maguire.
Imagine a second retina study using the same insurance claims database to compare bevacizumab and aflibercept for improving visual acuity (VA) one year after treatment for neovascular AMD. The researchers utilize two cohorts: those patients who receive only bevacizumab for the full year and those who receive only aflibercept for the full year.
That might sound sensible on the surface, said Dr. Maguire, but that would be concerning for retina specialists because, in today’s practice, patients often start on low-cost bevacizumab first and, if their vision doesn’t improve sufficiently, they are switched to aflibercept. Thus, in this example, “a set of patients doing poorly on bevacizumab would be excluded from the study because of the switch,” she said, “while every aflibercept patient doing poorly would be retained.” Bevacizumab would therefore appear to provide better VA. “The data are again hiding important information that the reader is not aware of,” Dr. Maguire added. “It sounds clean to use only patients who stayed on the same drug, but the data are still biased.”
The IRIS Registry
The Academy’s IRIS Registry has aggregated EHR information on 68 million patients from close to 16,000 participating clinicians. It includes a range of data points across 387 million patient visits, from demographics and medical history, to clinical examination findings, diagnoses, procedures, and medications.
Grants are available to clinicians and others who are interested in conducting IRIS Registry research.
Learn more at aao.org/iris-registry/data-analysis/requirements then scroll to “Current research opportunities.”
|
Keep Data Quality in Mind
“A large dataset like the IRIS Registry includes information in EHRs for patients across the United States,” said Leslie G. Hyman, PhD, at Wills Eye Hospital in Philadelphia. “But this information was captured for clinical, administrative, and reimbursement purposes, not specifically for research.
While these data can provide ophthalmologists with important information pertaining to diagnostics, exam findings, demographics, and treatment provided, they are not captured in a systematic, consistent manner across the board, she said. There can be missing data fields, data entry errors, and differing EHR formats, which cause high variability in the information available.
Cases for concern. “From a researcher’s perspective, it’s important to be aware of the data source and recognize the strengths and weaknesses of the dataset itself,” said Dr. Hyman. “That understanding drives how researchers will interpret the study findings, how the data apply to patients, and ultimately whether or not these large data sources allow researchers to answer the questions they want to pose.”
Scenario #1: Variable data. A good example of uneven data quality is the variability of VA measurements, said Dr. Hyman. VA is one of the most important pieces of information for evaluating the severity and impact of eye disease and treatment outcomes. In a traditional clinical study, researchers will measure VA using specific, standardized, detailed protocols, she said. But that’s often not the case in big datasets.
“Visual acuity measures captured by an EHR lack consistency,” said Dr. Hyman. For example, an eye care professional might measure acuity multiple times in a visit, with different methods, or when a patient is close to a target or far away. “Because of this variability, researchers have to think carefully about which of these measures best represent the visual acuity of a patient at a given time for a given visit,” in order for the study to be based on the most appropriate data, she said.
Scenario #2: Missing data. What if a researcher is interested in health disparities regarding the treatment of diabetic retinopathy, said Dr. Hyman, but 20% of the records in the dataset fail to include key information such as ethnicity of an individual, which is needed to answer the question?
“If researchers don’t have that vital information, they have to think about why it might be missing and how that might influence interpretation of the results,” said Dr. Hyman. Are there certain biases with respect to why people don’t report ethnicity? Would those reasons be related to having more severe disease or worse outcomes? Or is it just an omission? “Again, the investigator must consider the available data when posing a research question and make sure they are appropriate to the question that’s being asked,” she said.
With Big Data, Big Challenges
Big data applications such as the IRIS Registry are indeed providing unprecedented ways to investigate the natural history of disease, the prevalence of rare diseases, practice pattern changes, the diffusion of technology, and more, all in a cost-effective, real-world setting.
“Yet despite this tremendous promise, big data simply doesn’t have the answer for everything,” said Dr. Maguire. “These data studies are just difficult to do well given the different levels of expertise required—you need physicians, you need data scientists, you need experts in billing and coding.” Nevertheless, big data are becoming ubiquitous, she said, and as consumers, ophthalmologists need to be more mindful of when the answers are valuable and when they’re not, what they can tell us and what they can’t.
___________________________
1 Lisboa R et al. Ophthalmology. 2014;121(7):1317-1321.
2 Stacey AW et al. Invest Ophthalmol Vis Sci. 2012;53(4):1830-1834.
Meet the Experts
Leslie G. Hyman, PhD Vice chair for research at Wills Eye Hospital in Philadelphia. She is also the Thomas D. Duane Endowed Chair at the Sidney Kimmel Medical College of Thomas Jefferson University. Relevant financial disclosures: None.
Aaron Y. Lee, MD, MSc The Dan and Irene Hunter Associate Professor of Ophthalmology and vitreoretinal surgeon at the University of Washington in Seattle. Relevant financial disclosures: None.
Maureen G. Maguire, PhD, FARVO The Carolyn F. Jones Professor of Ophthalmology and biostatistician at the University of Pennsylvania’s Perelman School of Medicine in Philadelphia. Relevant financial disclosures: Dr. Maguire has received payment for serving on data and safety monitoring committees for Genentech and Regeneron.
Marion R. Munk, MD, PhD Professor and uveitis and medical retina specialist at the University Clinic Bern in Switzerland. She is also managing director of the Bern Photographic Reading Center and an adjunct lecturer at the Northwestern University in Chicago. Relevant financial disclosures: None.
For full disclosures and the disclosure key, see below.
Full Financial Disclosures
Leslie G. Hyman, PhD None.
Aaron Y. Lee, MD, MSc Carl Zeiss Meditech: S; FDA: E; Genentech: C; Gyroscope: C; Johnson & Johnson Vision: C; Microsoft: S; Nvidia: S; Santen: S; Verana Health C.
Maureen G. Maguire, PhD, FARVO Emmes: C; Foundation Fighting Blindness: S; Genentech: C; NEI: S.
Marion R. Munk, MD, PhD Acucela: C; Allergan: L; Bayer: C,S; Carl Zeiss: C,L; Gensight Therapeutics: C; Helbling: C; Isarna Therapeutics: C; Lumithera: C; Novartis: C,L; RetinaAI: C.
Disclosure Category
|
Code
|
Description
|
| Consultant/Advisor |
C |
Consultant fee, paid advisory boards, or fees for attending a meeting. |
| Employee |
E |
Employed by a commercial company. |
| Speakers bureau |
L |
Lecture fees or honoraria, travel fees or reimbursements when speaking at the invitation of a commercial company. |
| Equity owner |
O |
Equity ownership/stock options in publicly or privately traded firms, excluding mutual funds. |
| Patents/Royalty |
P |
Patents and/or royalties for intellectual property. |
| Grant support |
S |
Grant support or other financial support to the investigator from all sources, including research support from government agencies (e.g., NIH), foundations, device manufacturers, and/or pharmaceutical companies. |
|