Author: Daniel Palanker, PhD
The term LASER stands for Light Amplification by Stimulated Emission of Radiation. A beam of light is composed of individual packets of energy that are called quanta or photons. Each of these photons has a particular energy and direction of travel. The energy of a quantum of light is proportional to its frequency, ie, it is reciprocal of its wavelength. In the presence of a properly prepared laser material, it is possible for a quantum of light to trigger the release of other quanta with the same wavelength and direction of travel. This phenomenon is called stimulated emission, and it is an essential element in lasing. In thermal equilibrium the energy levels (E1, E2, etc.) of electrons in atoms and molecules are populated according to the Boltzmann distribution, relative to the ground level (E0): N1/N0 = exp(- E1 - E0/kT),
in which upper levels are always less populated than the lower levels (Figure 1).
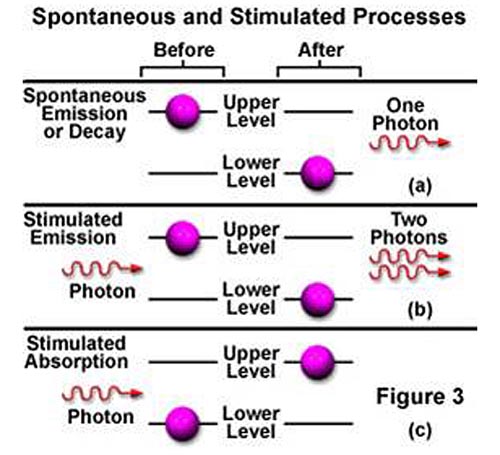
Figure 1. Stimulated emission and absorption in a laser.
Stimulated emission requires inversion of population between two energy levels, such that the upper level is more populated than the lower level (N2>N1). Such inversion of population can be achieved in materials having metastable levels of energy, with a lifetime of the exited state larger than that of a lower state (Figure 2), when material is excited out of the thermal equilibrium. Such nonequilibrium state is created in the lasing material by an excitation source or “pump.” An external photon passing through excited material can induce transition of an electron from excited state to a lower state, which is accompanied by emission of an identical photon. This process of stimulated emission enables light amplification, which can result in lasing.
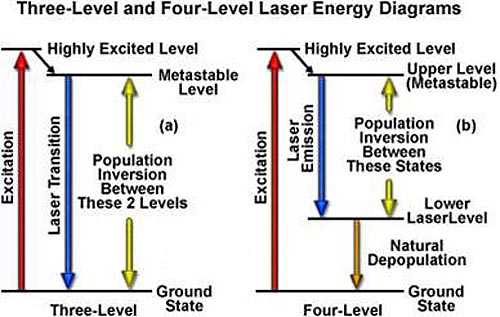
Figure 2: Population Inversion in a Laser
A laser is generally composed of three basic elements:
- A material that can store energy to be released by stimulated emission,
- A means of replenishing the energy stored in the excited laser material, and
- An optical resonator (cavity) for retaining a fraction of the light emitted by the lasing material to stimulate further emission.
Figure 3 schematically illustrates a general configuration of a laser. An energy source is used to introduce energy into the lasing material. This energy is stored as atomic or molecular excitation waiting to be released by stimulated emission. Laser light that has already been emitted by the lasing material circulates between the two mirrors on either end of the laser cavity, with a fraction of the light escaping through one mirror to form the laser beam. The trapped light stimulates emission of new quanta of light from the laser material with the same wavelength and direction as the original quanta (Animation 1). In this way, a laser produces a beam of light between the two mirrors in which all of the quanta move “in phase” with one another. This property of light is called coherence.
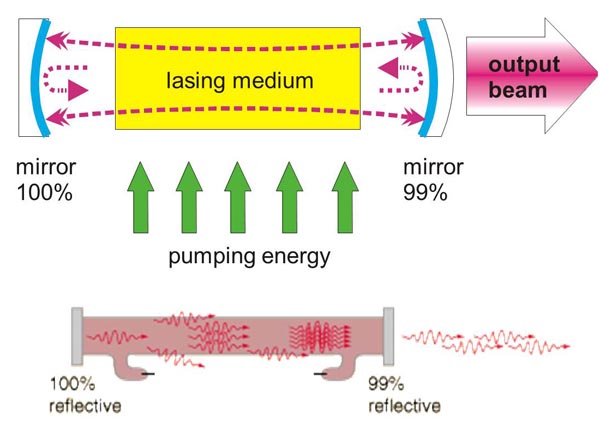
Figure 3. Laser configuration.
Coherence is related to synchronization of light in time, or along the laser beam. The duration of the synchronized emission from the laser multiplied by the speed of light is called the coherence length of the laser emission. This is the distance along which the photons are coherent or moving “in step.” To remain in phase with one another, these quanta must have approximately the same wavelength. Thus temporal coherence is related to the monochromaticity (or spectral width) of the light emitted from the laser: the broader the spectrum the shorter the temporal coherence. A laser may produce one or several discrete spectral lines in either the infrared, visible, or ultraviolet domains. This is in contrast to conventional light sources (incandescent or arc lamps), which typically produce noncoherent polychromatic (broad-band or white) light.
Collimation (directionality) of the emitted beam is governed by the mirror configuration of the laser cavity. In its simplest form, a cavity consists of two mirrors arranged such that light bounces back and forth, each time passing through the gain medium. One of the two mirrors, the output coupler, is partially transparent, allowing the output beam to exit through it (Figure 3). The reflection coefficient of the output coupler determines how many times photons are reflected back to circulate inside the cavity before exiting it. For example, with a reflection coefficient of 0.99, the photon will bounce on average 99 times before exiting the cavity. The structure of the laser cavity determines directionality (collimation) of the laser beam, which determines its ability to be focused into a small spot.
The lasing (or gain) medium can be a gas, liquid, or solid. Lasers can be pumped by continuous discharge lamps and by pulsed flash lamps, by electric discharges in the laser medium, by chemical reactions, by an electron beam, by direct conversion of electric current into photons in semiconductors, or by light from other lasers. Laser pulse durations can vary from femtoseconds to infinity (continuous). Pulsing techniques used for different ranges of pulse durations include electronic shutters (down to 1 ms), pulsed flash lamps (typically down to a few ms), Q-switching (down to a few ns), or mode locking (down to fs).
Resulting laser beam is coherent (photons are emitted in-phase), monochromatic (narrow spectral width), and collimated (directional). Most common medical lasers are listed in Table 1.
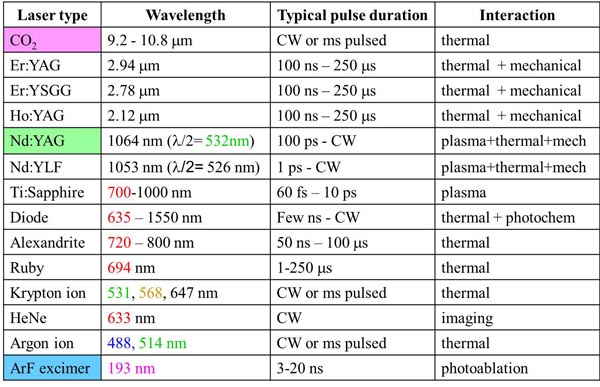
Table 1. Common lasers in medicine.
Laser Beam Delivery to Tissue
Laser beams are typically very well collimated. Diffraction causes light waves to spread transversely as they propagate, and it is therefore impossible to have a perfectly collimated beam. The diffraction-limited divergence angle of a Gaussian beam with diameter D and wavelength λ is Θ = 4 ⋅ λ/Π ⋅ D. As an example, for an Argon laser emitting a 1 mm wide beam at 515 nm wavelength, the divergence (half-angle Q) is about 0.66 mrad, ie, the beam spreads by 1.3 mm over a distance of 1 meter.
Using a lens or a concave mirror with focal length f, a laser beam can be focused to a spot with a diameter d = (4 ⋅ f/Π ⋅ D)λ. The depth of the focal region is: F = (8 ⋅ f2/Π ⋅ D2)λ (Figure 4). With a f=25 mm lens the same Argon laser beam can be focused to a spot of 16 mm in diameter, having a focal depth of 820mm. It must be emphasized though that exact definition of the spot size depends on the beam profile, which varies in various configurations of laser cavities. For therapeutic laser photocoagulation such tight focusing is usually not required, and laser spots typically vary in diameter between 50 and 500 mm in various applications.
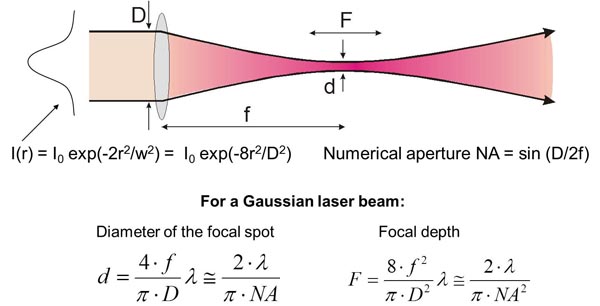
Figure 4. Laser beam focusing.
As an alternative to a free-propagating beam, laser light can be transported via optical fibers. An optical fiber, schematically shown in Figure 5, typically consists of a core, cladding, and jacket. Light is trapped within the core due to total internal reflection at the interface of core with cladding. To satisfy conditions of total internal reflection, the incidence angle of light at the core/cladding interface should not exceed the critical angle of total internal reflection: sin Θcr = ncore/nclad, where ncore and nclad are refractive indices of the core and cladding, respectively. To satisfy these criteria for total internal reflection, the light should be launched within a so called acceptance cone, and the sine of its half-angle Θac is defined as the numerical aperture (NA) of the fiber: NA = sin Θac = square root of n2core - n2clad. Typically the NA is within a range of 0.1-0.2. Optical fibers are often used for delivery of laser light to slit-lamp-based systems and to the intraocular surgical probes.
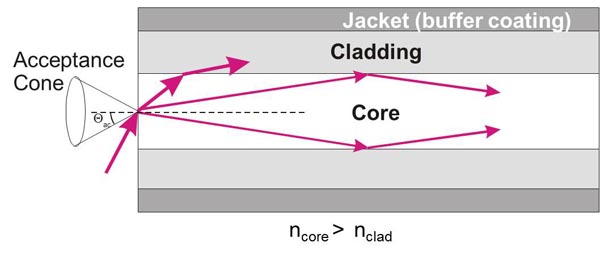
Figure 5. Fiber delivery of the laser beam.